2.2 Carnaval de Matemáticas – Teoría del Caos
¿Qué es lo que denominan caos? ¿A qué se refieren y por qué hay quienes piensan que es importante? Comencemos con estas preguntas y otras similares.
El concepto de caos es uno de los más excitantes y rápidamente extendidos en los tópicos de investigación de las décadas recientes. Ordinariamente, el caos es desorden o confusión. En el sentido científico, el caos involucra algo de desorden, pero es mucho más que eso.
El caos que se estudia es una clase particular de cómo cambia algo con el tiempo. De hecho, cambio y tiempo son los aspectos fundamentales que juntos conforman la fundación del caos. El clima, la bolsa de valores, los precios de los alimentos y el tamaño de las poblaciones de insectos, por ejemplo, cambian con el tiempo (En la jerga del caos, se les conoce como sistemas; un sistema es un ensamblaje de partes interactuando, como el sistema del clima; alternativamente, es un grupo o secuencia de elementos, especialmente en la forma de un cronológicamente ordenado conjunto de datos; comenzaremos a expresarnos en términos de sistemas a partir de este momento). Las cuestiones básicas que nos llevan al descubrimiento del caos están basadas en el cambio y en el tiempo. Por ejemplo ¿Cuál es el comportamiento cualitativo a largo plazo de un sistema cambiante? O, dado nada más un registro de cómo algo ha cambiado con el tiempo ¿Cuánto podemos aprender sobre el sistema subyacente? Por lo tanto, “el comportamiento con el tiempo” será nuestro tema.
¿Por qué es importante? Brevemente, si tu trabajas con mediciones numéricas (Datos), el caos puede ser importante porque su presencia significa que las predicciones a largo plazo no tienen sentido y son estériles. El caos también ayuda a explicar el comportamiento irregular de algo que a través del tiempo. Finalmente, cualquiera que se tu campo, vale la pena estar familiarizado con las nuevas orientaciones y nuevos temas interdisciplinarios (Como el caos) que juegan un papel prominente en diversas áreas.
La forma más fácil para ver como algo cambia con el tiempo es realizar un gráfico. El peso de un bebe, por ejemplo, podría cambiar como lo muestra la figura 1 (a). La figura 1 (b) es un gráfico hipotético mostrando como fluctúa el precio del trigo a través del tiempo.
Figura 01
Aún cuando la gente no realice ninguna medición numérica, pueden simular una serie de tiempo utilizando alguna regla específica, usualmente una ecuación matemática. La ecuación describe como una cantidad cambia de un estado de inicio conocido. La figura 1 (b) es un ejemplo generado siguiendo la siguiente ecuación:
Ecuación 01
Donde xt (Se expresa “x de t”) es el valor de x a un tiempo t, y xt+1 (x de t más uno) es el valor de x a un intervalo de tiempo (Día, año, siglo, etc.) posterior. Esto muestra uno de los requisitos para el caos: el valor a cualquier tiempo depende en parte de un valor previo. Para generar una serie de tiempo caótico con la ecuación 01, primero asignamos (Arbitrariamente) el valor “1” para xt y utilizamos la ecuación para calcular xt+1.
Solo por observar la serie de tiempo de la figura 1 (b), nadie puede decir si es o no caótica. En otras palabras, el observar comportamiento errático temporal es solo un indicador superficial de posible caos. Solo un análisis detallado de los datos puede revelar si la serie es caótica.
La serie de tiempo simulada en la figura 1(b) tiene varias características clave:
-
Muestra complejidad, movimiento no sistemático (incluyendo cambios rápidos y súbitos), más que una simple curva, tendencia, ciclo o equilibrio (Una posible analogía es que muchos sistemas evolutivos en nuestro mundo muestran inestabilidad, convulsiones, sorpresas, innovación perpetua y eventos radicales).
-
El patrón indiscriminado no viene de un proceso accidental, como unas esferas fuera de un tazón. Al contrario, viene de una ecuación específica. Por lo tanto, una secuencia caótica luce accidental pero realmente es determinista, significa que sigue una regla. Esto es, alguna ley, ecuación o procedimiento determina o especifica el resultado. Además, para valores dados de las constantes y aportes, los resultados futuros son predecibles.
-
La ecuación que generó el comportamiento caótico es simple. Por consiguiente, el comportamiento complejo no necesariamente tiene un origen complejo.
-
El comportamiento caótico viene con una sola variable (x). Esto es, el caos no tiene que venir de la interacción de muchas variables, con una sola se puede.
-
El patrón es enteramente auto-generado. En otras palabras, está separado de cualquier otra influencia o se desarrolló sin ninguna influencia externa.
-
La evolución irregular viene sin la influencia directa de muestreos o medición del error en los cálculos (No hay términos de error en la ecuación).
La revelación del comportamiento desorganizado y complejo puede venir de una elemental, determinista ecuación o causa subyacente simple que sea una sorpresa para muchos científicos. Curiosamente, varios campos de estudio, han aceptado una idea afín: Las colecciones de pequeñas entidades (Partículas o lo que sea) se comportan sin orden ni concierto a pesar de que las leyes físicas gobiernan a las partículas individuales.
La ecuación 01 muestra el porque muchos científicos se sienten atraídos al caos: El comportamiento que luce complejo y aún imposible de descifrar y entender, puede ser relativamente sencillo y comprensible. Otra de las atracciones es que muchos de los conceptos básicos del caos no requieren de matemáticas avanzadas, como cálculo, ecuaciones diferenciales, variable compleja, etc. Por el contrario, mucho de esta teoría se puede comprender con álgebra básica, geometría plana y quizás algo de estadística rudimentaria. Finalmente, otro punto es que, para analizar el caos, no tenemos que conocer las ecuaciones que gobiernan el sistema.
El caos es un campo joven y en rápido desarrollo. De hecho, mucha de su información fue descubierta a principios de la década de 1970. Como resultado, muchos aspectos del caos están lejos de ser entendidos o resueltos. La materia más importante sin resolver es probablemente esta: En el presente, el caos es extremadamente difícil de identificar en la información del mundo real. Ciertamente aparece en ejercicios matemáticos y en algunos experimentos de laboratorio. Sin embargo, hay en la actualidad un gran debate acerca de si alguien ha identificado claramente el caos en datos de campo. En cualquier caso, no podemos simplemente tomar un poco de datos, aplicar una prueba simple o dos y declarar “Caos” o “No Caos”.
La descripción y la teoría del caos, están muy adelantados con respecto a la identificación del caos en la información del mundo real. Sin embargo, con la popularidad actual del caos como un tópico de investigación, nuevos y mejores métodos están emergiendo con regularidad.
Carnaval de Matemáticas:


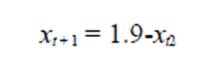
Interesante entrada, esto de medir el caos siempre me hace pensar. Que opinas de esto, si alguien pudiera invertir la entropía total del universo y llegar al resultado caos=0, ese alguien sería Dios?
Saludos.
Gracias por visitar y comentar Rojo Merlín.
Pues si, si alguien pudiese realizar esa modificación y lo que implica, debería ser una entidad suprema, sin duda.