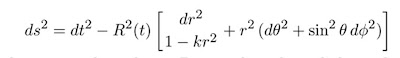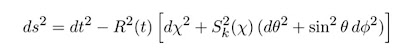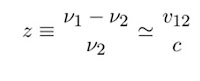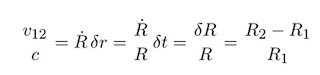Cosmología del Big Bang. Parte 01
Introducción al Modelo Estándar.
La expansión observada del Universo es un resultado natural (Casi inevitable) de cualquier modelo cosmológico homogéneo e isotrópico basado en la relatividad general. Sin embargo, por sí mismo, la expansión de Hubble no proporciona la evidencia suficiente para lo que nosotros generalmente nos referimos como el modelo cosmológico del Big Bang. Mientras la relatividad general es en principio capaz de describir la cosmología de cualquier distribución de materia, es extremadamente afortunado de que nuestro Universo aparezca como homogéneo e isotrópico en grandes escalas. Juntos, la homogeneidad y la isotropía nos permiten extender el Principio de Copérnico al Principio Cosmológico afirmando que todas las posiciones espaciales en el Universo son esencialmente equivalentes.
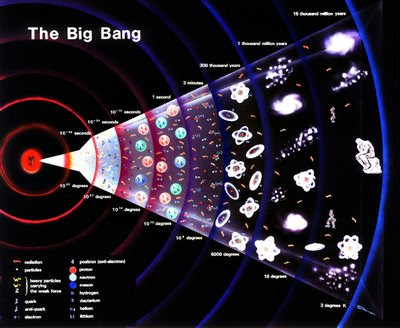
La formulación del modelo del Big Bang inicia en la década de 1940 con el trabajo de George Gamow y sus colaboradores, Alpher y Herman. Con el fin de dar cuenta de la posibilidad de la abundancia de elementos tiene un origen cosmológico, esto propone que el Universo primitivo fue una vez muy caliente y denso (Lo suficiente para permitir el proceso de nucleosíntesis del hidrógeno) y se expandió y enfrió a su estado actual. En 1948, Alpher y Herman predijeron que una consecuencia directa de este modelo es la presencia de un vestigio de radiación de fondo con una temperatura del orden de unos pocos Kelvin. Por supuesto, esta radiación se observó 16 años después que la radiación cósmica de fondo. De hecho, esta fue la observación de la radiación de 3 K que señaló al modelo del Big Bang como el primer candidato para describir nuestro Universo. El trabajo subsecuente en la nucleosíntesis del Big Bang adicional, confirmó la necesidad de un pasado caliente y denso. Los modelos cosmológicos relativistas enfrentan serios problemas con sus condiciones iniciales para los cuales la mejor solución moderna es la cosmología inflacionaria, de la cual platicaré en un ‘post’ posterior. De ser correcto, estas ideas podrían hacer que el término ‘Big Bang’ sea redundante, desde que fue acuñado por Hoyle para representar una crítica de la falta de comprensión de las condiciones iniciales.
El Universo de Robertson-Walker
La homogeneidad e isotropía observadas nos permiten describir la geometría general y la evolución del Universo en términos de dos parámetros cosmológicos estimados para la curvatura espacial y la expansión general (o contracción) del Universo. Estas dos cantidades aparecen en la mayoría de las expresiones generales para las métricas del espacio-tiempo las cuales tienen un (3D) sub-espacio máximo simétrico de un espacio-tiempo 4D, conocida como la métrica de Robertson-Walker:
Nótese que adoptamos c=1 en todo. Ajustando la base de la coordenada radial, podemos escoger la constante de curvatura k, para tomar solo los valores discretos +1, -1, o 0 que corresponden a geometrías cerradas, abiertas o espaciales planas. En este caso, frecuentemente es más conveniente re-expresar la métrica como:
(Ec.2)
Donde la función Sk (X) es (Sen X, X, Senh X) para k = (-1, 0, +1). La coordenada r (En la Ec. 1 y el ‘ángulo’ X en la Ec. 2 son ambos adimensionales. Las dimensiones están asignadas a R(t), la cual es el factor de la escala cosmológica que determina las distancias apropiadas en términos de coordinadas móviles. Una alternativa común es definir un factor de escalas dimensionales, a(t) = R(t)/R0, donde R0 ≡ R (t0) es R en la época presente. Es también conveniente en ocasiones definir un tiempo adimensional o de coordenadas de tiempo conformes, η, por dη = dt/R(t). A lo largo de constantes secciones espaciales, el tiempo adecuado es definido por la coordenada de tiempo, t. Similarmente, para dt= dΦ = dφ= 0, la distancia adecuada es dada por R(t)x.
El desplazamiento al rojo
El desplazamiento al rojo cosmológico es una consecuencia directa de la expansión Hubble, determinada por R(t). Un observador local detecta luz de un emisor a distancia y ve un desplazamiento al rojo en la frecuencia. Podemos definir al desplazamiento al rojo como
(Ec. 3)
Donde V1 es la frecuencia de la luz emitida, V2 es la frecuencia observada y V12 es la velocidad relativa entre el emisor y el observador. Mientras la definición z=(V1-V2)/V2 es válida en todas las distancias escalares, relacionar el desplazamiento al rojo con la velocidad relativa es simple solo en escalas pequeñas (Menor que las escalas cosmológicas) como la velocidad de expansión es no relativista. Para señales de luz, podemos utilizar la métrica otorgada en la Ec. 1 y ds2=0 para escribir:
(Ec. 4)
Donde δr(δt) es la coordenada radial (temporal) de separación entre el emisor y el observador. De este modo, obtenemos la relación simple entre el desplazamiento al rojo y el factor escalar:
(Ec. 5)
Este resultado no depende de la aproximación no relativista.
Bueno, por hoy, aquí concluiremos, en el siguiente post, hablaremos de las Ecuaciones de Movimiento de Friedmann – Lemaître y la Definición de los Parámetros Cosmológicos.
(Ec.1)